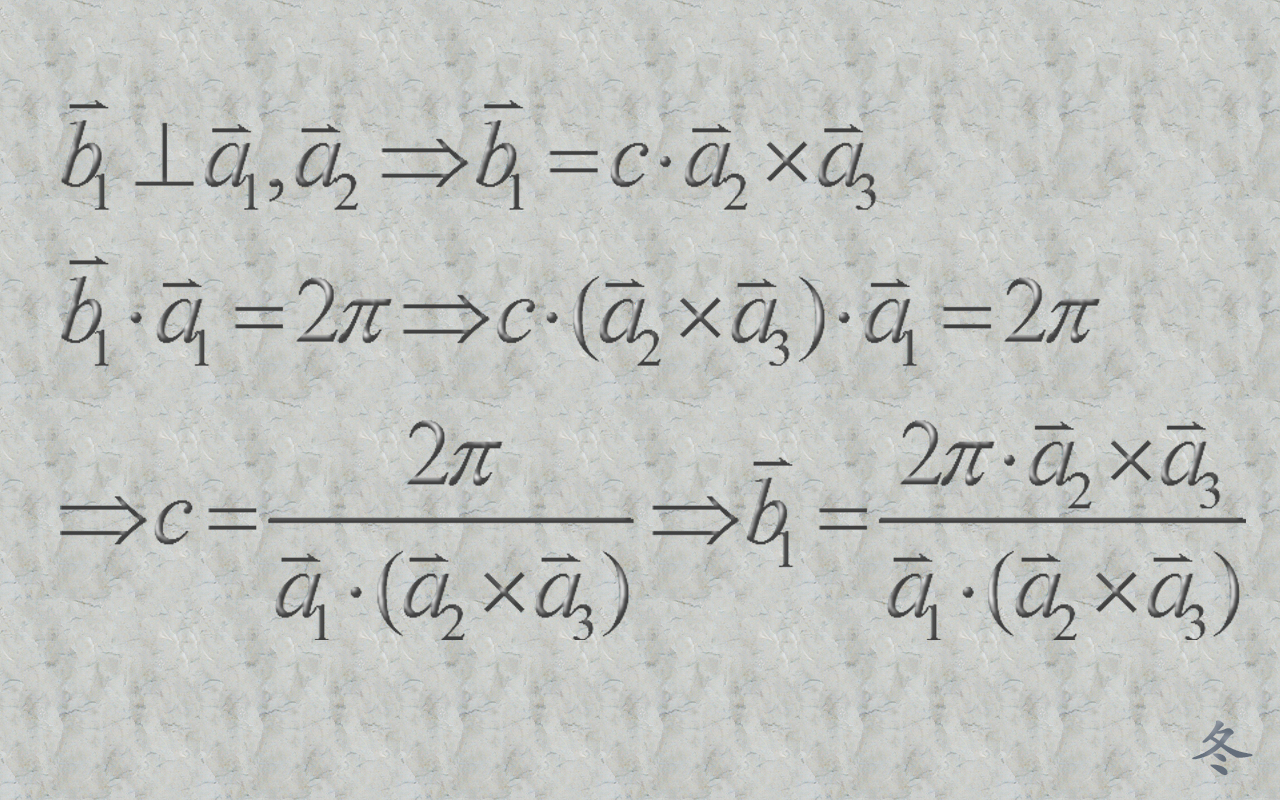Spaepen covered six parts in his class Solids: Structure and Defects: 1) type of bonding, 2) formal description of structure, 3) diffraction, 4) phase equilibria, 5) structure and stability of metallic phases, and 6) defects. In doing so, he managed to combine related topics in crystallography, X-ray diffraction, thermodynamics, and metallurgy in a single course. This course serves as a foundation for students enrolled in materials sciences who have little or no materials science background.

I chose to audit this class partly because the topics are relevant to my research, and partly because I was curious how an evaluation of 4.8 out of 5 is possible. People who had taken it before me said that it is one of the most demanding courses, but despite the complaints, they unanimously agreed that it is a great course. So I went to the first class, on a Tuesday, and against my nature, at 8:30 in the morning. What impressed me the most was that Spaepen actually wrote on the blackboard using a chalk. After a few lectures, I began to think how all physics lectures should be done with a chalk and a blackboard, and that here is an example of how it is done properly.

I spent the past two days reviewing the lecture notes and handouts from the class. After almost a year, I have forgotten most of the details, but several small derivations still caught my eyes. They were the ah-hah moments in the lectures and were usually questions that had puzzled me for quite some time in my graduate school. Among them, the definition of reciprocal lattice is one, and the geometrical representation of Fourier pairs is another.

I have learned the formalism of how to define the basis of a reciprocal lattice from various books, but no one seem to bother giving any explanation on why it is so defined. I had assumed that it probably involves some lengthy derivations that no one wants to put into textbooks. But with five lines of Maths (see the image of curved equations), Spaepen showed how and why it is so defined. It is the first genuine moment of “why I haven’t thought about it before”.

Fourier analysis is a subject that I picked up here and there from various sources, mostly in optics and solid state physics. Its application to crystal analysis is one that I always wanted to learn, but never had the chance to learn it properly. Sitting through that part of the course gave me such an opportunity, and it turned out to be a joyous experience . It helped me to combine the old subject with a new (to me) technique. The geometrical insights on diffraction relates the abstract geometrical representation of Fourier pairs to physical reality through a familiar technique X-ray diffraction. The geometrical representation helped me solve several long-standing crystallographic puzzles that I had in explaining diffraction patterns of thin films of mesoporous materials.

The last two parts of the lecture were unfamiliar territory for me. Listening to these parts of the lectures, I realized how difficult the course must have been for people who had no prior knowledge on materials science at all. Chewing the materials once again, I can grasp the general outlines of the materials. I guess I will really learn them if I need to use them one day.